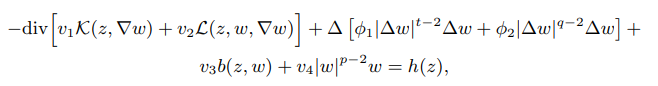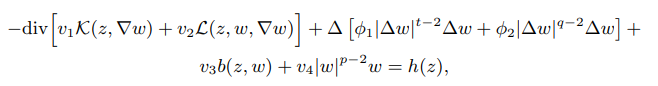TY - JOUR
T1 - Study of Certain Navier Problems in Sobolev Space with Weights
AU - Fadil , Y.
AU - Ouaarabi , M. El
AU - Oukessou , M.
JO - Journal of Nonlinear Modeling and Analysis
VL - 4
SP - 1332
EP - 1352
PY - 2025
DA - 2025/07
SN - 7
DO - http://doi.org/10.12150/jnma.2025.1332
UR - https://global-sci.org/intro/article_detail/jnma/24237.html
KW - Navier problem, degenerate quasilinear elliptic equations, weighted
Sobolev spaces, weak solution.
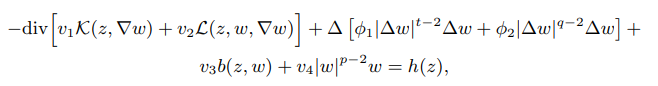
AB - <p style="text-align: justify;">In this paper, we study the following Navier problem<br/></p><p style="text-align:center"><img src="https://admin.global-sci.org/uploads/ueditor/image/20250710/1752112429546666.png" title="1752112429546666.png" alt="image.png" width="641" height="76"/></p><p style="text-align: justify;">Here, $h ∈ L^{p&#39;} (\mathcal{Q}, v^{1−p′}_1),$ $\mathcal{K}, \mathcal{L}$ and $b$ are Carathéodory functions and $ϕ_1,ϕ_2,$ $v_1,
v_2, v_3$ and $v_4$ are $A_p$-weights functions. By using the theory of monotone operators (Browder–Minty Theorem), we demonstrate the existence and uniqueness
of weak solution to the above problem.<br/></p>