Commun. Math. Anal. Appl., 4 (2025), pp. 179-201.
Published online: 2025-06
Cited by
This paper is concerned with a fully parabolic Patlak-Keller-Segel-Navier-Stokes system
where $Ω ⊂\mathbb{R}^2$ is a smoothly bounded domain and the parameter $χ$ is positive.
The main aim of this note is to show that if
then the solution of the above system is global and bounded in time.
- BibTex
- RIS
- TXT
This paper is concerned with a fully parabolic Patlak-Keller-Segel-Navier-Stokes system
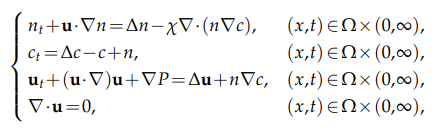
where $Ω ⊂\mathbb{R}^2$ is a smoothly bounded domain and the parameter $χ$ is positive.
The main aim of this note is to show that if
then the solution of the above system is global and bounded in time.
This paper is concerned with a fully parabolic Patlak-Keller-Segel-Navier-Stokes system
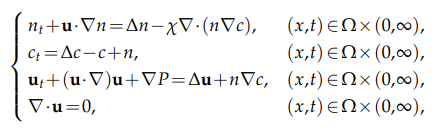
where $Ω ⊂\mathbb{R}^2$ is a smoothly bounded domain and the parameter $χ$ is positive.
The main aim of this note is to show that if
then the solution of the above system is global and bounded in time.